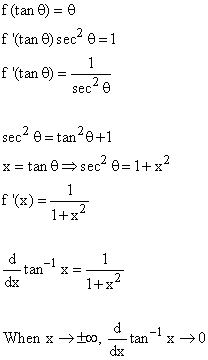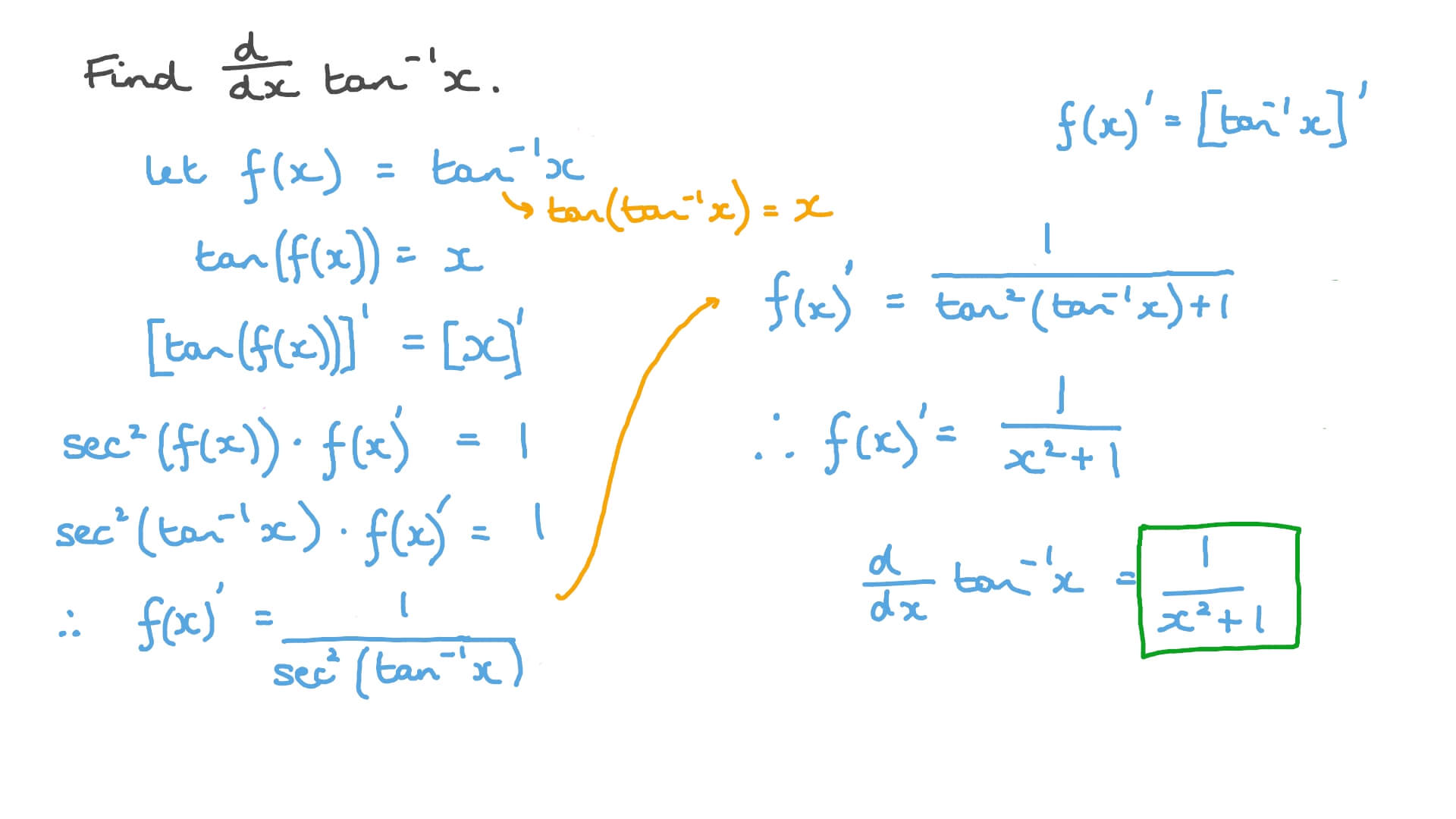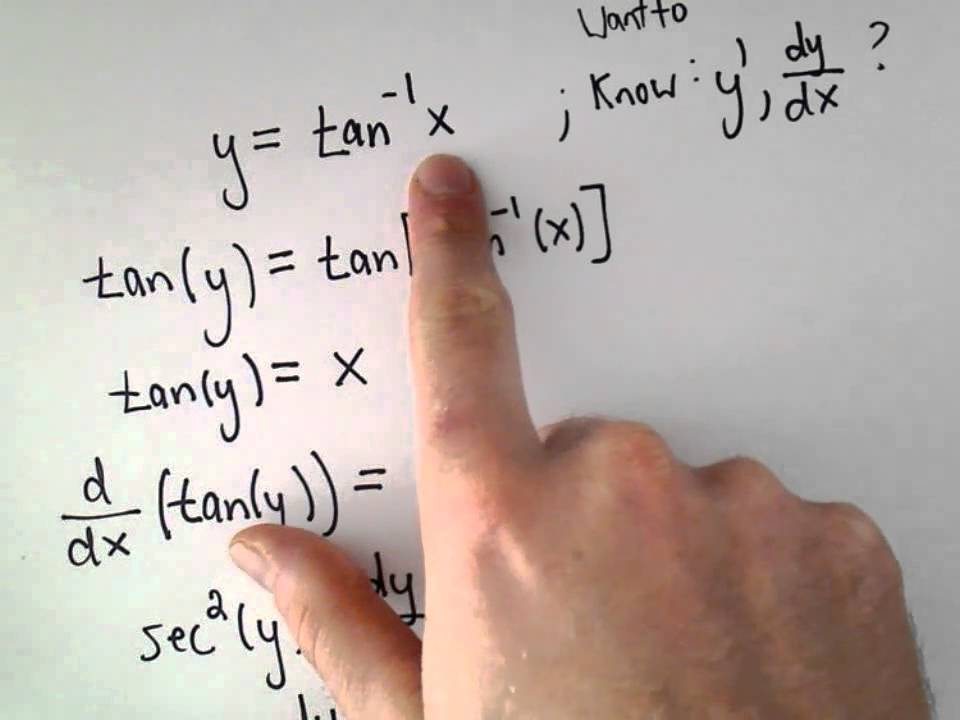Derivative Of Tan 1 X
Ln x2 1 cos x tan 1 x etc.
Derivative of tan 1 x. This might appear to conflict logically with the common semantics for expressions such as sin 2 x which refer to numeric power rather than function composition and. Let s get straight into an example and talk about it after. Is the area of the region in the xy plane bounded by the graph of f the x axis and the lines x a and x b such that area above the x axis adds to the total and that below the x axis subtracts from the total.
Resultant force 5 x cos 20 8 x cos 25 2 5 x sin 20 8 x sin 25 2 13 n direction angle of resultant force tan 1 5 x sin 20 8 x sin 25 5 x cos 20 8 x cos 25 23 the direction angle of resultant force is calculated from the resultant of two forces acting at an angle. Derivative of inverse tangent. What is x cos x dx.
X3 x cosx x2 1. So for the maximum area the semicircle on top must have a radius of 1 6803 and the rectangle must have the dimensions 3 3606 x 1 6803 h x 2 r. V cos x so now it is in the format u v dx we can proceed.
In mathematics the definite integral. U x 1. The notations sin 1 x cos 1 x tan 1 x etc as introduced by john herschel in 1813 are often used as well in english language sources conventions consistent with the notation of an inverse function.
Let f x tan 1 x then. X2 1 etc. U is the derivative of the function u x as a diagram.
Note that in the above examples log differentiation is not required but makes taking the derivative easier allows you to avoid using multiple product and quotient rules use whenever you are trying to differentiate d dx f x g x examples. Ok we have x multiplied by cos x so integration by parts is a good choice. We can also see that the second derivative is always negative in fact it s a constant and so we can see that the maximum area must occur at this point.
First choose which functions for u and v.